Chapter 3: Answers 2 Jack K. Cohen Colorado School of Mines
-
A(r) = πr2, so
 = 2πr. This says that
= 2πr. This says that
 = C, the circumference of the circle—if you stop to think, this makes geometric sense.
= C, the circumference of the circle—if you stop to think, this makes geometric sense.
- Evaluate the previous result for

 21.99 m when r = 3.5 m.
21.99 m when r = 3.5 m.
- (3.1.31)
A = πr2, C = 2πr. Eliminate
r = C/(2π) to get
A(C) = C2/(4π). So,
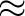 = C/(2π).
= C/(2π).
-
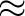
 0.56 m when C = 3.5 m.
0.56 m when C = 3.5 m.
- (3.1.32) The implication is that r increases at a constant rate, so r = 5t ft. Thus
A(t) = πr2 = 25πt2 ft2 and
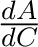 = 50πt ft2/sec. When t = 10, we have
= 50πt ft2/sec. When t = 10, we have
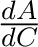 = 500π ft2/sec.
= 500π ft2/sec.
- (Generalization of Example 6)
- At the maximum height, v = 0, so
t = ttop = v0/g and
stop = v02/(2g).
- At ground level, s = 0, so
0 = - gt2/2 + v0t = t(v0 - gt/2). The t = 0 root corresponds to the initial time, so the other root gives the final time,
tf = 2v0/g. Thus, the final velocity is
vf = - g⋅2v0/g + v0 = - v0.
- The initial and final velocities are equal in magnitude and opposite in direction (no matter what the initial velocity is—there is nothing special about the text's choice of 96 ft/sec).
- The dimensions of the result,
stop = v02/(2g) are
(
 )2÷
)2÷ = L which is correct. The dimensions of
vf = - v0 are obviously the dimensions of a velocity, so this checks as well.
= L which is correct. The dimensions of
vf = - v0 are obviously the dimensions of a velocity, so this checks as well.
- Re the inverse square law:
- Yes! When s = 0, we see from the given formula for s that
vf2 = v02, so again the final and initial velocities have the same magnitude.
- At the maximum height, v = 0, so
stop =
 .
.
- With the given numbers, the constant force law gives
stop = 144 ft and the inverse square result gives 144.001 ft. Thus for velocities of this order of magnitude, we can ignore the effect of the inverse square law unless unusually high precision is demanded.
- Re the water bucket problem:
- The given function expands to the quadratic
10 - t/5 + t2/1000, so
V'(t) = - 1/5 + t/500. Since t is measured in seconds, we evaluate
V(60) = 8/5 = 1.6.
- The average change is
(V(100) - V(0))/(100 - 0) = (0 - 10)/100 = - 1/10. Equating this to V'(t) gives the linear equation
-1/10 = - 1/5 + t/500 with solution t = 50 sec.
- No, it would imply that the bucket magically refills to 10 liters after all the water has leaked out. It wasn't really asked, but a good scientist routinely checks that problems makes sense. In this case, for example, is V(0) = 10 as asserted? Is
V(100) = 0 as asserted?
- (3.1.36) Your figure should look something like Figure 1. The graph is virtually linear and you can get sufficient accuracy by just computing the change over the 2 year period 1974-1976 which gives a growth rate of 17 thousand/year. Using some very fancy curve fitting tools I got 17.0031 which is, indeed, 17 to the accuracy of the given data.
Figure:
Curve fit of population data.
 |
 = 2πr. This says that
= 2πr. This says that
 = C, the circumference of the circle—if you stop to think, this makes geometric sense.
= C, the circumference of the circle—if you stop to think, this makes geometric sense.

 21.99 m when r = 3.5 m.
21.99 m when r = 3.5 m.
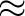 = C/(2π).
= C/(2π).
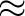
 0.56 m when C = 3.5 m.
0.56 m when C = 3.5 m.
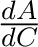 = 50πt ft2/sec. When t = 10, we have
= 50πt ft2/sec. When t = 10, we have
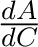 = 500π ft2/sec.
= 500π ft2/sec.
 )2÷
)2÷ = L which is correct. The dimensions of
vf = - v0 are obviously the dimensions of a velocity, so this checks as well.
= L which is correct. The dimensions of
vf = - v0 are obviously the dimensions of a velocity, so this checks as well.
 .
.
